树 Tree
数组、链表与树
- 数组通过下标来访问元素,速度快,对于有序数组可以利用二分查找,但是如果插入一个节点,会整体移动,效率低
- 链式存储便于删除、添加,在检索时只能从头/尾开始遍历查找
- 树能提高存储、读取的效率,既可以保证检索的速度,也可保证数据插入、删除、修改的速度
树的常用术语(详见wikipedia.org Tree_(data_structure)):
- Neighbor
Parent or child. - Ancestor
A node reachable by repeated proceeding from child to parent. - Descendant
A node reachable by repeated proceeding from parent to child. Also known as subchild. - Degree
For a given node, its number of children. A leaf has necessarily degree zero. - Degree of tree
The degree of a tree is the maximum degree of a node in the tree. - Distance
The number of edges along the shortest path between two nodes. - Level
The level of a node is the number of edges along the unique path between it and the root node. This is the same as depth when using zero-based counting. - Width
The number of nodes in a level. - Breadth
The number of leaves. - Forest
A set of one or more disjoint trees. - Ordered tree
A rooted tree in which an ordering is specified for the children of each vertex. The book The Art of Computer Programming uses the term oriented tree. - Size of a tree
Number of nodes in the tree.
二叉树 Binary Tree
- 每个节点最多只能有两个子节点
- 二叉树的节点分为左节点和右节点
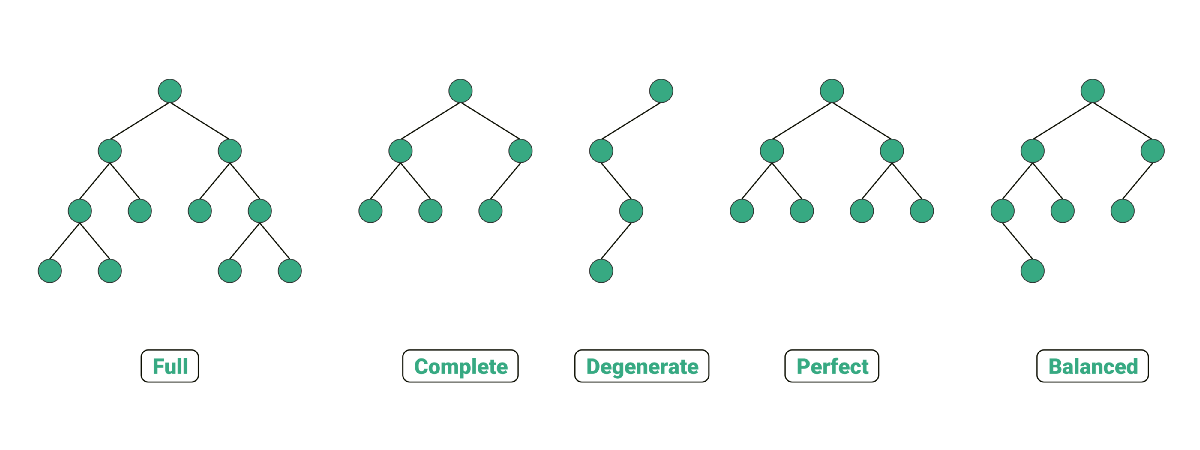
- 如果二叉树的所有叶子节点都在最后一层,节点总数为 2^n-1 称为满二叉树
- 如果二叉树的所有叶子节点都在最后一层或倒数第二层;最后一层从左边连续,倒数第二层从右边连续,称为完全二叉树
注:中英文翻译存在区别,perfect 被译为满二叉树,full 译为完满二叉树,可参照 Different Types of Binary Tree with colourful illustrations
深度优先遍历
根据父节点的位置,遍历分为:前序、中序、后序
- 前序遍历:1、输出父节点;2、遍历左子树;3、遍历右子树
- 中序遍历:1、遍历左子树;2、输出父节点;3、遍历右子树
- 后续遍历:1、遍历左子树;2、遍历右子树;3、输出父节点
前序遍历 Pre-Order Traversal
- 输出当前节点,
- 如果左子节点不为空则递归继续前序遍历
- 如果右子节点不为空,则递归继续前序遍历
中序遍历 In-Order Traversal
- 如果左子节点不为空,则递归继续中序遍历
- 输出当前节点
- 如果右子节点不为空,则递归继续中序遍历
后序遍历 Post-Order Traversal
- 如果左子节点不为空,则递归继续后序遍历
- 如果右子节点不为空,则递归继续后序遍历
- 输出当前节点
public class binaryTreeDemo {
public static void main(String[] args) {
//create a binary tree
BinaryTree binaryTree = new BinaryTree();
HeroNode node1 = new HeroNode(1,"a");
HeroNode node2 = new HeroNode(2,"b");
HeroNode node3 = new HeroNode(3,"c");
HeroNode node4 = new HeroNode(4,"d");
/*
HeroNode node5 = new HeroNode(5,"e");
node3.setLeft(node5);
*/
node1.setLeft(node2);
node1.setRight(node3);
node3.setRight(node4);
binaryTree.setRoot(node1);
/*
* node1
* / \
* node2 node3
* \
* node4
* */
System.out.println("pre");
binaryTree.preOrder();
System.out.println("----------");
System.out.println("in");
binaryTree.inOrder();
System.out.println("----------");
System.out.println("post");
binaryTree.postOrder();
}
}
class BinaryTree {
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
}else {
System.out.println("null");
}
}
public void inOrder() {
if (this.root != null) {
this.root.inOrder();
}else {
System.out.println("null");
}
}
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
}else {
System.out.println("null");
}
}
}
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"id=" + no +
", name='" + name + '\'' +
'}';
}
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
public void inOrder() {
if (this.left != null) {
this.left.inOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.inOrder();
}
}
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
}运行上述代码得到:
pre
HeroNode{id=1, name='a'}
HeroNode{id=2, name='b'}
HeroNode{id=3, name='c'}
HeroNode{id=4, name='d'}
----------
in
HeroNode{id=2, name='b'}
HeroNode{id=1, name='a'}
HeroNode{id=3, name='c'}
HeroNode{id=4, name='d'}
----------
post
HeroNode{id=2, name='b'}
HeroNode{id=4, name='d'}
HeroNode{id=3, name='c'}
HeroNode{id=1, name='a'}思考:如果在 node3 的左边添加一个 node5,前、中、后序遍历的顺序是什么
- 前序:1-2-3-5-4
- 中序:2-1-5-3-4
- 后序:2-5-4-3-1
查找 Search
使用不同方法查找 node5 看看分别比较了几次。(前序4次,中序3次,后序2次)
前序查找 Pre-Order Search
- 当前节点的 no 是否等于要查找的,相等,则返回当前节点
- 不等,则判断左子节点是否为空,不为空则递归前序查找
- 如果左递归前序查找,找到了则返回,否则继续判断当前结点的右子节点是否为空,如果为空继续向右递归查找
中序查找 In-Order Serach
- 则判断左子节点是否为空,不为空则递归中序查找
- 当前节点的 no 是否等于要查找的,相等,则返回当前节点
- 如果左递归前序查找,找到了则返回,否则继续判断当前结点的右子节点是否为空,如果为空继续向右递归查找
后序查找 Post-Order Serach
- 则判断左子节点是否为空,不为空则递归中序查找
- 如果左递归前序查找,找到了则返回,否则继续判断当前结点的右子节点是否为空,如果为空继续向右递归查找
- 当前节点的 no 是否等于要查找的,相等,则返回当前节点
在之前的代码对应的类上添加以下内容
/* main method
HeroNode result = binaryTree.preSearch(5);
if (result != null) {
System.out.println("found, id:" + result.getNo() + " name:" + result.getName());
} else {
System.out.println("not found");
}
*/
class BinaryTree {
public HeroNode preSearch(int no) {
if (root != null) {
return root.preSearch(no);
} else {
return null;
}
}
public HeroNode midSearch(int no) {
if (root != null) {
return root.midSearch(no);
} else {
return null;
}
}
public HeroNode postSearch(int no) {
if (root != null) {
return root.postSearch(no);
} else {
return null;
}
}
}
class HeroNode {
public HeroNode preSearch(int no) {
if (this.no == no) {
return this;
}
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.preSearch(no);
}
if (resNode != null) {
return resNode;
}
if (this.right != null) {
resNode = this.right.preSearch(no);
}
return resNode;
}
public HeroNode midSearch(int no) {
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.midSearch(no);
}
if (resNode != null) {
return resNode;
}
if (this.no == no) {
return this;
}
if (this.right != null) {
resNode = this.right.midSearch(no);
}
return resNode;
}
public HeroNode postSearch(int no) {
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.postSearch(no);
}
if (resNode != null) {
return resNode;
}
if (this.right != null) {
resNode = this.right.postSearch(no);
}
if (this.no == no) {
return this;
}
return resNode;
}
}顺序存储二叉树
背景
从数据结构来看,数组的储存方式和树的储存方式可以互相转换 ,即数组既可以转换成树,树也可以转换成数组。
- 二叉树的节点以数组 int[] array 的方式来存放
- 遍历数组 array 时,仍然可以以前、中、后序遍历的方式完成节点遍历
- 顺序二叉树 通常只考虑 完全二叉树
- 第 n 个元素的 左子节点为 2n+1
- 第 n 个元素的 右子节点为 2n+2
- 第 n 个元素的 父节点为 (n-1)/2
n为数组的 index,通过上面的方法就可以实现两者的相互转换
代码
对于一个数组{1,2,3,4,5,6,7}要求以二叉树前序遍历的方式进行遍历,得到的结果应为 1,2,4,5,3,6,7
/*
* 1
* / \
* 2 3 ------> {1,2,3,4,5,6,7}
* / \ / \
* 4 5 6 7
*
* */
public class arrayTree {
public static void main(String[] args) {
int[] array = {1, 2, 3, 4, 5, 6, 7};
ArrTraversal arrTraversal = new ArrTraversal(array);
System.out.println("pre order");
arrTraversal.preOrder();
System.out.println();
System.out.println("mid order");
arrTraversal.midOrder();
System.out.println();
System.out.println("post order");
arrTraversal.postOrder();
}
}
class ArrTraversal {
private int[] array;
public ArrTraversal(int[] array) {
this.array = array;
}
public void preOrder(){
this.preOrder(0);
}
public void midOrder(){
this.midOrder(0);
}
public void postOrder(){
this.postOrder(0);
}
public void preOrder(int index) {
if (array == null || array.length == 0) {
System.out.print("Array is NULL!");
}
System.out.print(array[index]);
if ((2 * index + 1) < array.length) {
preOrder(2 * index + 1);
}
if ((2 * index + 2) < array.length) {
preOrder(2 * index + 2);
}
}
public void midOrder(int index) {
if (array == null || array.length == 0) {
System.out.print("Array is NULL!");
}
if ((2 * index + 1) < array.length) {
midOrder(2 * index + 1);
}
System.out.print(array[index]);
if ((2 * index + 2) < array.length) {
midOrder(2 * index + 2);
}
}
public void postOrder(int index) {
if (array == null || array.length == 0) {
System.out.print("Array is NULL!");
}
if ((2 * index + 1) < array.length) {
postOrder(2 * index + 1);
}
if ((2 * index + 2) < array.length) {
postOrder(2 * index + 2);
}
System.out.print(array[index]);
}
}线索化二叉树
背景
对通过下面这个数组构建一个二叉树,每个元素(节点)都有 2 个指针 left 和 right 指向子节点,但是对于 8,10,14,6 而言它们的指针没有被完全利用,指针为空。
/*
* {1,3,6,8,10,14}
*
* 1
* / \
* 3 6
* / \ /
* 8 10 14
*
**/n 个节点的二叉树链表中含有 n+1 个空指针域,推导公式:2n-(n-1) = n+1
利用二叉链表中的空指针域,存放指向该节点在 某种遍历次序下的 前驱 和 后继 节点的指针,这种附加的指针称为“线索”,例如:将 节点 8 的右指针指向 前驱 节点 3 。
这种加上了线索的二叉树链表称为 线索链表(节点存储了下一个节点,组成了链表,并且一般的二叉树本来就是用链表实现的),相应的二叉树称为 线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为:前、中、后序线索二叉树。
代码
将下面的二叉树进行中序线索化
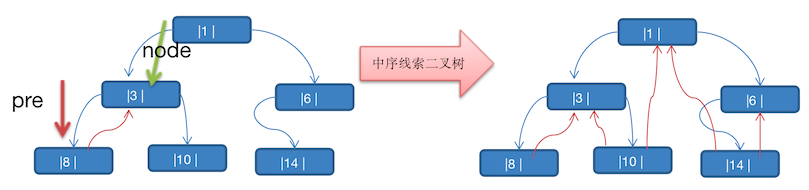
依靠数组{8,3,10,1,14,6}可知:
- 8 的后继节点为 3
- 3 由于左、右指针都使用了,不能线索化
- 10 的前驱节点为 3,后继节点为 1
- 1 不能线索化
- 14 的前驱节点为 1,后继节点为 6
- 6 有左节点,不能线索化
当二叉树线索化后,有如下情况:
- left 指向的是 左子树,也可能是指向 前驱节点 例如:节点 1 left 节点指向的是左子树,节点 10 的 left 指向的就是前驱节点
- right 指向的是 右子树,也可能是指向 后继节点 例如:节点 3 的 right 指向的是右子树,节点 10 的 right 指向的是后继节点
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
HeroNode node1 = new HeroNode(1,"a");
HeroNode node2 = new HeroNode(3,"b");
HeroNode node3 = new HeroNode(6,"c");
HeroNode node4 = new HeroNode(8,"d");
HeroNode node5 = new HeroNode(10,"e");
HeroNode node6 = new HeroNode(14,"f");
node1.setLeft(node2);
node1.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(node1);
threadedBinaryTree.threadedNode(node1);
HeroNode leftNode = node5.getLeft();
System.out.println("parent of node5: " + leftNode);
HeroNode rightNode = node5.getRight();
System.out.println("child of node5: " + rightNode);
}
}
class ThreadedBinaryTree {
private HeroNode root;
//pointer
//pre point to parent node
private HeroNode pre;
public void setRoot(HeroNode root) {
this.root = root;
}
public void threadedNode(){
this.threadedNode(root);
}
//threaded
public void threadedNode(HeroNode node) {
if (node == null) {
return;
}
//threaded left subtree
threadedNode(node.getLeft());
//threaded this node
//point to parent node
if (node.getLeft() == null) {
//left pointer point to parent node
node.setLeft(pre);
//chang type of this pointer
node.setLeftType(1);
}
//child node
if (pre != null && pre.getRight() == null) {
pre.setRight(node);
pre.setRightType(1);
}
pre = node;
//threaded right subtree
threadedNode(node.getRight());
}
}
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
//leftType: 0: left is point to left subtree
// 1: left is point to parent node
//rightType: 0: right is point to right subtree
// 1:right is point to child node
private int leftType; // leftType == 0: left subtree, leftType == 1: parent
private int rightType; // rightType == 0: right subtree, rightType == 1: child
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"id=" + no +
", name='" + name + '\'' +
'}';
}
}遍历中序线索化二叉树
- 对于中序遍历,一直往左找,直到 left 为 null 时,则是打印的第一个节点
- 然后看它的 right 指针类型,是否为线索化节点,是的话则打印 right 指向的节点
- right 如果是一个普通节点,那么就直接处理它的右侧节点
在 ThreadedBinaryTree 类中加入下面这个方法,在测试类或主方法中直接调用这个方法。
public void threadedList() {
HeroNode tempNode = root;
while (tempNode != null) {
// find leftType == 1
while (tempNode.getLeftType() == 0) {
tempNode = tempNode.getLeft();
}
System.out.println(tempNode);
while (tempNode.getRightType() == 1) {
tempNode = tempNode.getRight();
System.out.println(tempNode);
}
tempNode = tempNode.getRight();
}
}堆排序 Heap Sorting
背景
- 堆排序是一种选择排序,它的最坏、最好、平均时间复杂度均为O(nlogn),是不稳定排序。
- 堆:是一种完全二叉树(complete)
- 每个节点的值都大于或等于其左右子节点的值称为大顶堆
- 每个节点的值都小于或等于其左右子节点的值称为小顶堆
(对左右两个子节点的位置关系没有要求)
使用大顶堆进行升序排序,小顶堆进行降序排序
堆排序的方法
- 将待排序序列构造成一个大顶堆
注意:这里使用的是数组,而不是一颗二叉树 - 此时:整个序列的最大值就是堆顶的根节点
- 将堆顶元素与末尾元素进行交换,此时末尾就是最大值
- 然后将剩余 n-1 个元素重新构造成一个堆,就会得到 n 个元素的次小值。如此反复,便能的得到一个有序序列
可以看到在构建大顶堆的过程中,元素个数逐渐减少,最后得到一个有序序列。
举例:对数组 {4,6,8,5,9} 进行堆排序,将数组升序排序。
大顶堆的构建
数组对应的树结构如下:
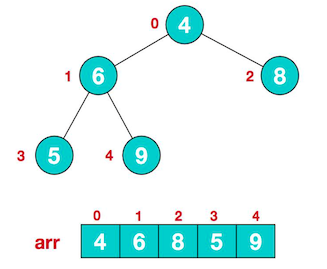
此时从最后一个非叶子节点开始调整,从左到右,从上到下进行调整。叶节点不用调整,对于数组中:第一个非叶子节点 arr.length/2-1 = 5/2-1=1 ,arr[1] = 6 。
比较它与它的两个子节点,找出最大值,将最大值与它交换。
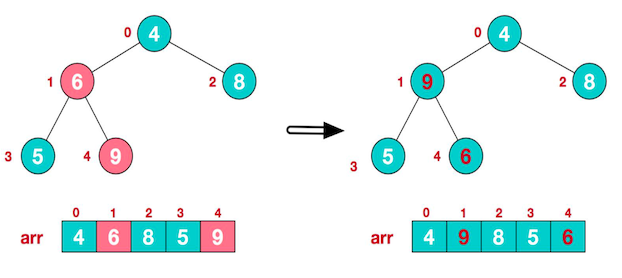
找到第二个非叶子节点 4 ,4、9、8 中 9 最大,将其与4交换
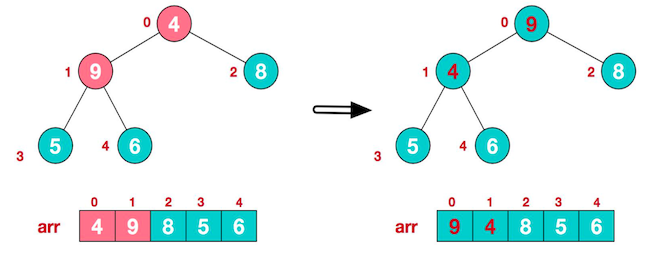
由于交换了 4 和 9 ,子树发生改变,还需要再比较 4、5、6 ,其中 6 最大,将4和6交换位置。
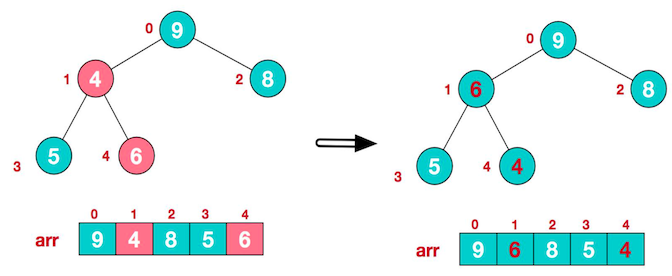
此时构建出了同一个大顶堆
交换元素
将堆顶元素与末尾元素进行交换,使其末尾元素最大。然后继续调整,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
将堆顶元素 9 与末尾元素 4 进行交换
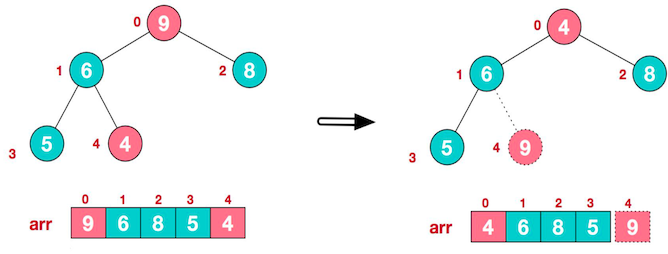
最大元素 9 已经在数组的末尾,接下来按照上述方法再次进行排序,此时非叶子节点是4,4、6、8 中 8 最大,与 4 交换位置。
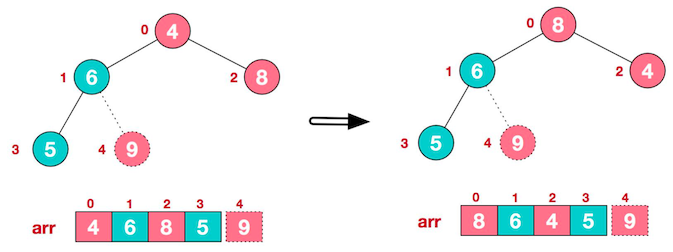
再将堆顶的 8 与 5 交换位置,得到第二大元素
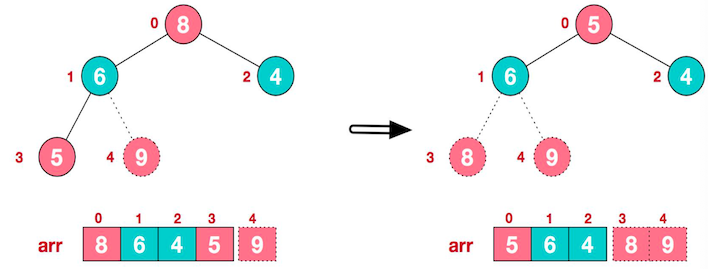
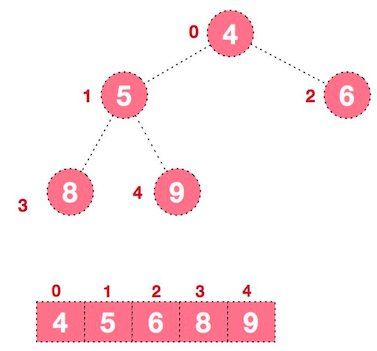
如此往复(6最大,与5交换后,和最小元素4对调)最后得到有序序列
代码
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] array = {4, 6, 8, 5, 9};
Sort sort = new Sort();
sort.heapSort(array);
System.out.println(Arrays.toString(array));
}
}
class Sort {
public void heapSort(int[] array) {
int temp;
for (int i = array.length/2-1; i >= 0; i--) {
adjustHeap(array,i,array.length);
}
for (int j = array.length-1; j >0 ; j--) {
temp = array[j];
array[j] = array[0];
array[0] = temp;
adjustHeap(array, 0, j);
}
}
public void adjustHeap(int[] array, int i, int length) {
int temp = array[i];
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) { // make the biggest one on the top
if (k + 1 < length && array[k] < array[k + 1]) { //left node < right node
k++; //k point to the bigger one(right)
}
if (array[k] > temp) { //if child > parent
array[i] = array[k];
i = k;
} else {
break;
}
}
array[i] = temp;
}
}赫夫曼树 Huffman Tree
背景
- 给定 n 个权值作为 n 个叶子节点,构造一颗二叉树,若该树的带权路径长度(WPL, weighted path length)达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree),也翻译为霍夫曼树。
- 赫夫曼树是带全路径长度最短的树,权值较大的节点离根节点较近
基础概念
- 路径:在一颗树中,从一个节点往下可以到达的孩子或孙子节点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根节点的层数为 1,则从根节点到第 L 层节点的路径长度为 L-1
- 节点的权:若将树中节点赋给一个有着某种含义的数值,则这个数值称为该节点的权。
- 节点的带权路径长度为:从根节点到该节点之间的路径长度与该节点的权的乘积。
- 树的带权路径长度:所有叶子节点的带权路径长度之和,记为 WPL(weighted path length),权值越大的节点离根节点越近的二叉树才是最优二叉树
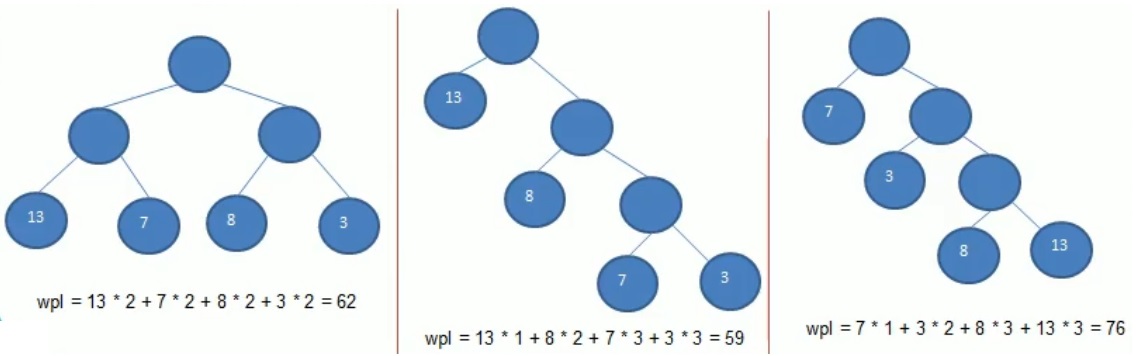
中间的 WPL 最小,则为 Huffman tree
赫夫曼树的创建
方法
给一个数列 {13,7,8,3,29,6,1} 转换成一颗赫夫曼树
- 升序排序,每个数据是一个节点,每个节点可以看出一颗最简单的二叉树(两个子节点为空)
- 取出根节点权值最小的两棵二叉树
- 组成一棵新二叉树,该二叉树的根节点是前面两颗二叉树根节点权值的和
- 在将这棵新的二叉树以根节点的权值大小再次排序以此往复,直到所有的数据都处理过
对于上面的例子:
/*
* 38
* / \
* 15 23
* / \ / \
* 10 7 8 10 13
* / \ / \
* 4 4 6 4 6
* / \ -> / \ -> / \
* 1 3 1 3 1 3
*
*
* 87
* / \
* 29 38
* / \
* 15 23
* / \ / \
* -> 7 8 10 13
* / \
* 4 6
* / \
* 1 3
* */代码
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = {13, 7, 8, 3, 29, 6, 1};
createHuffmanTree(arr);
Node root = createHuffmanTree(arr);
preOrder(root);
}
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("null");
}
}
public static Node createHuffmanTree(int[] arr) {
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
//sort
Collections.sort(nodes);
//System.out.println(nodes);
// get two smallest nodes
Node leftNode = nodes.get(0);
Node rightNOde = nodes.get(1);
// create a binary tree
Node parent = new Node(leftNode.value + rightNOde.value);
parent.left = leftNode;
parent.right = rightNOde;
//delete these nodes in arraylist
nodes.remove(leftNode);
nodes.remove(rightNOde);
//add parent to arraylist
nodes.add(parent);
}
return nodes.get(0);
}
}
class Node implements Comparable<Node> {
int value;
Node left;
Node right;
public void preOrder() {
System.out.print(this+",");
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return value + "";
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}使用前序遍历对转化好的赫夫曼树进行打印,验证结果。
输出
运行上述程序可得到 67,29,38,15,7,8,23,10,4,1,3,6,13 符合推导出的赫夫曼树。
赫夫曼编码 Huffman Coding
背景
- 赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种 编码方式,属于一种 程序算法
- 赫夫曼编码是 赫哈夫曼树 在电讯通信中的经典的应用之一
- 赫夫曼编码广泛地用于 数据文件压缩。其压缩率通常在 20%~90% 之间
- 赫夫曼码是 可变字长编码(VLC) 的一种。Huffman 于 1952 年提出一种编码方法,称之为最佳编码
举例
定长编码
// 原始字符,共40个字符(包括空格)
i like like like java do you like a java
// 对应 Ascii 码
105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97
// Ascii 码对应的二进制
01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 01110110 01100001
//总的长度是 359 (包括空格)变长编码
// 原始字符,共40个字符(包括空格)
i like like like java do you like a java
// 各个字符对应的个数
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9
// 按照各个字符出现的次数进行编码,原则是出现次数越多的,则编码越小,比如"空格"出现了 9 次, 编码为 0 ,其它依次类推.
// 等号前面的数字就是就是赫夫曼树节点的带权路径
0= , 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u, 1010=y, 1011=d按照上面给各个字符规定的编码,长度会变短,字符的编码都不能是其他字符编码的前缀,符合此要求的编码叫做前缀编码,即不能匹配到重复的编码。对于变长编码,存在匹配的多义性。
赫夫曼编码
获得对应字符对应的个数后,以各数字出现的次数作为权值,构建一个赫夫曼树。根据赫夫曼树的路径给各个字符编码。(规定,向左是0,向右是1)这是一个前缀编码,即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性。
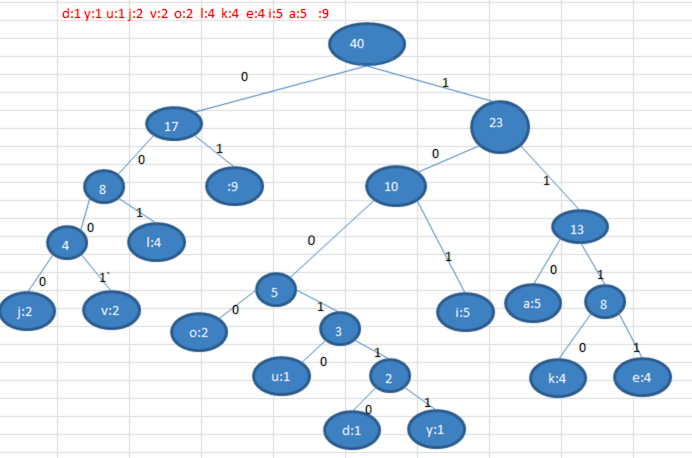
o: 1000 u: 10010 d: 100110 y: 100111 i: 101
a: 110 k: 1110 e: 1111 j: 0000 v: 0001
l: 001 : 01转换成对应的赫夫曼编码
1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110赫夫曼编码长度为133,使用定长编码时,长度为359,赫夫曼编码是无损处理方案
赫夫曼树的排序方法不同(权值相同时),得到的赫夫曼编码不一样,但是wpl是一样的,长度相同。
赫夫曼编码的实现
用上面的例子,将 “i like like like java do you like a java” 转换为赫夫曼编码
创建赫夫曼树
- 创建 Node,具有如下属性:
data:存放对应的字符
weight:该字符出现的总次数
left:左节点
right:右节点 - 得到字符串对应的数组
- 创建数组对应的节点,放到 List 中,形式{[Node[date=7,weight=5]],[Node[date=32,weight=9]…}
- 创建对应的赫夫曼树
二叉排序树 Binary Search(Sort) Tree
背景
对于一个数列{7,3,10,12,5,1,9}要高效地完成查找和添加。可视化 https://visualgo.net/zh/bst
任何一个非叶子节点,左子节点 < 父节点,右子节点 > 父节点,相同值可以放在左或右边(本例中放在左边)。因此,对于中序遍历,刚好为升序排序。
以根节点计算,BST 的所有左子树的值均小于右子树的值
创建和遍历
public class BinarySortTree {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9};
BinarySearchTree binarySearchTree = new BinarySearchTree();
for (int i = 0; i < arr.length; i++) {
binarySearchTree.add(new Node(arr[i]));
}
binarySearchTree.inOrder(); //1,3,5,7,9,10,12
}
}
class BinarySearchTree {
private Node root;
public void add(Node node) {
if (root == null) {
root = node;
return;
} else {
root.add(node);
}
}
public void inOrder() {
if (root != null) {
root.inOrder();
} else {
System.out.println("null");
}
}
}
class Node {
int value;
Node left;
Node right;
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//construct
public Node() {
}
public Node(int value) {
this.value = value;
}
//add Node
public void add(Node node) {
if (node == null) {
return;
}
//compare
//if node < root node of the subtree
if (node.value < this.value) {
if (this.left == null) { // do not hava left child node
this.left = node;
} else { // find next
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
}
public void inOrder() {
if (this.left != null) {
this.left.inOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.inOrder();
}
}
}
删除
删除节点分为两种情况
- 删除叶子节点
- 删除只有一个子树的节点
- 删除有多个子树的节点
1、删除叶子节点的方法
- 找到要删除的节点
- 找到目标节点的父节点
- 判断是左子节点还是右子节点
- 删除对应的指针
2、对应的,删除只有一个子树的节点,直接用子节点代替当前节点
3、对于删除具有两个子树的节点
- 需要对树结构破坏最小
- 找到一个继任节点(successor)
- 在左子树寻找最大值 或 在右子树寻找最小值
- 使用 successsor 代替当前节点
完整实现
代码中的注释已包含所有内容。
import java.util.Objects;
/*
* 7
* / \
* 3 10
* / \ / \
* 1 5 9 12
* \ / / \
* 6 8 11 13
* */
public class BinarySortTree {
public static void main(String[] args) {
BinarySearchTree binarySearchTree = new BinarySearchTree();
int[] arr = {7, 3, 10, 12, 5, 1, 9, 6, 8, 11, 13};
for (int j : arr) {
binarySearchTree.add(new Node(j));
}
binarySearchTree.inOrder();
System.out.println("recursion search parent is: " + binarySearchTree.recursionSearchParent(1));
System.out.println("iterate search parent is: " + binarySearchTree.whileSearchParent(1));
Node searchNode = binarySearchTree.recursionSearchNode(10);
System.out.println("result: " + searchNode);
System.out.println("left: " + searchNode.getLeft() + "\n" + "right: " + searchNode.getRight());
Node targetNode = binarySearchTree.recursionSearchNode(10);
binarySearchTree.deleteNode(targetNode);
binarySearchTree.inOrder();
}
}
class BinarySearchTree {
Node root;
/**
* Add a node to BST
*
* @param node the node to add
*/
public void add(Node node) {
if (node == null) {
System.out.println("Node is null");
} else {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
}
/**
* in Order the whole BST recursively
*/
public void inOrder() {
if (root == null) {
System.out.println("root is null!");
return;
}
root.inOrder();
System.out.println();
}
/**
* get the parent of a node
*
* @param searchValue a child node
* @return parent node
*/
public Node recursionSearchParent(int searchValue) {
if (searchValue == root.value) {
return null;
}
return root.recursionSearchParent(searchValue);
}
/**
* get the parent of a node
*
* @param searchValue a child node
* @return parent node
*/
public Node whileSearchParent(int searchValue) {
if (searchValue == root.value) {
return new Node();
}
return root.whileSearchParent(searchValue);
}
/**
* search the node
*
* @param searchValue the value want to search
* @return a node and the node's value equals the search value
*/
public Node recursionSearchNode(int searchValue) {
return root.recursionSearchNode(searchValue);
}
/**
* delete a node
*
* @param targetNode a node to delete, can generate by recursionSearchNode()
*/
public void deleteNode(Node targetNode) {
if (Objects.equals(targetNode, root)) { //if it is root node
Node successor = root.searchSuccessor(targetNode); //find the successor
Node successorParent = targetNode.whileSearchParent(successor.value); //find the parent of the successor
targetNode.value = successor.value; //change the root.value
if (successor.value > successorParent.value) { //judge successor is right or left sub node
// then remove the parent's pointer
successorParent.right = null;
} else {
successorParent.left = null;
}
} else { //if it is not a root node
root.deleteNode(targetNode);
}
}
}
class Node {
int value;
Node left;
Node right;
public Node getLeft() {
return left;
}
public Node getRight() {
return right;
}
//constructor
public Node() {
}
public Node(int value) {
this.value = value;
}
/**
* add a node to BST
*
* @param node a node to add
*/
public void add(Node node) {
if (node == null) {
System.out.println("Node is null");
} else {
if (this.value < node.value) {
if (this.right == null) {
this.right = node;
} else {
right.add(node);
}
} else {
if (this.left == null) {
this.left = node;
} else {
left.add(node);
}
}
}
}
/**
* inorder, sorted
*/
public void inOrder() {
if (this.left != null) {
this.left.inOrder();
}
System.out.print(this.value + ",");
if (this.right != null) {
this.right.inOrder();
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
/**
* search a node's parent
*
* @param value node's value
* @return parent node
*/
public Node recursionSearchParent(int value) {
//search from a node to the leaf node
//one of child node's value == value, return this node
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
//search right
if (this.value < value && this.right != null) {
return right.recursionSearchParent(value);
}
//search left
if (this.value >= value && this.left != null) {
return left.recursionSearchParent(value);
}
}
//not found
return new Node();
}
/**
* search a node's parent
*
* @param searchValue the node's value
* @return parent node
*/
public Node whileSearchParent(int searchValue) {
Node tempNode = this;
while (true) { //find until leaf node
if (tempNode.left != null && tempNode.left.value == searchValue || tempNode.right != null && tempNode.right.value == searchValue) {
return tempNode;
} else if (tempNode.value < searchValue && tempNode.right != null) {
tempNode = tempNode.right;
} else if (tempNode.value >= searchValue && tempNode.left != null) {
tempNode = tempNode.left;
} else if (tempNode.left == null && tempNode.right == null) {
return new Node();
}
}
}
/**
* search a node
*
* @param value node's value
* @return the node, which value == value
*/
public Node recursionSearchNode(int value) {
if (this.value == value) {
return this;
}
if (this.value < value && this.right != null) {
return this.right.recursionSearchNode(value);
}
if (this.value > -value && this.left != null) {
return this.left.recursionSearchNode(value);
}
return null;
}
/**
* delete a node in BST
* only use this method can not delete root node
*
* @param targetNode a node to delete, can generate by recursionSearchNode()
*/
public void deleteNode(Node targetNode) {
Node targetNodeParent = recursionSearchParent(targetNode.value);
//case 0 targetNode is a leaf node
if (targetNode.left == null && targetNode.right == null) {
if (targetNode.value > targetNodeParent.value) {
targetNodeParent.right = null;
} else {
targetNodeParent.left = null;
}
}//case 1 targetNode has one sub node
else if (targetNodeParent.right == null && targetNodeParent.left != null || targetNodeParent.right != null && targetNodeParent.left == null) {
if (targetNodeParent.value < targetNode.value) { //targetNode on the right of parent
targetNodeParent.right = searchSuccessor(targetNode);
} else { //targetNode on the left
targetNodeParent.left = searchSuccessor(targetNode);
}
}//case 2 targetNode has two sub nodes
else {
//get successor and successor's parent
Node successor = searchSuccessor(targetNode);
Node successorParent = recursionSearchParent(successor.value);
// delete the pointer to successor
if (Objects.equals(successorParent.right, successor)) {
successorParent.right = null;
} else {
successorParent.left = null;
}
// make the target node parent point to successor
if (Objects.equals(targetNodeParent.right, targetNode)) {
targetNodeParent.right = successor;
} else {
targetNodeParent.left = successor;
}
//make the pointer point to original node
successor.left = targetNode.left;
successor.right = targetNode.right;
}
}
/**
* look for successor, smallest in right subtree (inorder successor)
* the biggest in left subtree also can work (predecessor)
*
* @param targetNode a node want to find successor
* @return the node's successor
*/
public Node searchSuccessor(Node targetNode) {
Node successor;
//case 0
if (targetNode.left != null && targetNode.right == null) {
return targetNode.left;
}
if (targetNode.left == null && targetNode.right != null) {
return targetNode.right;
}
//case 1
if (targetNode.left != null) { // now (targetNode.right != null) is always true
successor = targetNode.right;
while (successor.left != null) {
successor = successor.left;
}
return successor;
}
//if (targetNode.left==null && targetNode.right==null)
return null;
}
}平衡二叉树 AVL Tree
背景
以发明者 Adelson-Velsky 和 Landis 的名字命名,对于一个数组 {1,2,3,4,5,6} 创建一个二叉排序树,则其更像是一个单链表,左子树全部为空,极大降低了查找速度(速度不如单链表)
1
\
2
\
4
\
6AVL 树在二叉排序树的基础上实现,AVL 树的左右两个子树的高度的绝对值差不超过1,左右两个子树也都是 AVL 树,平衡二叉树的实现方法有:红黑树、AVL、替罪羊树、Treap、伸展树等
AVL 算法
为了将一棵 BST 转化为 AVL ,需要计算树的高度、实现左旋转、右旋转和双旋转
树的高度计算
AVL 算法关键的一个程序是:获得树的最大高度(Height),也叫深度(Depth),也就是根节点到最远的叶子节点的路径长度。下面这个写法非常巧妙。
public int getDepth() {
return Math.max(left == null ? 0 : left.getDepth(), right == null ? 0 : right.getDepth()) + 1;
}
public int getLeftDepth() {
if (left == null) {
return 0;
} else {
return left.getDepth();
}
}
public int getRightDepth() {
if (right == null) {
return 0;
} else {
return right.getDepth();
}
}利用递归,不断查找最深的位置,每次弹出的时候会在后面加1,并返回较大的那个数,再在此基础上继续弹出。然后获得最大的那个数。
同样的,对于左右两个子树,使用一样的方法,只是初始节点不同。
左旋转
当 右子树深度 – 左子树深度 > 1 时,进行左旋转,将其换为 AVL 树。
将树进行一次左旋转,添加一个新节点,然后对新、根 2 个节点的值、左、右指针(6个变量)进行修改。
- 创建一个新的节点(newNode),值与当前根节点(rootNode)相同
newNode.value = rootNode.value - 把新节点的左指针设为 rootNode 的左指针指向的节点
newNode.left = rootNode.left - 把新节点的右指针设为 rootNode 的右指针的左指针指向的节点
newNode.rigt = rootNode.right.left - 把 rootNode 的值设为它的右指针指向节点的值
rootNode.value = rootNode.right.value - 把 rootNode 的右指针设为它的右指针的右指针指向的节点
rootNode.right = rootNode.right.right - 把 rootNode 的左指针设为新节点 newNode
rootNode.left = newNode
public void leftRotate() {
Node newNode = new Node(this.value);
newNode.left = this.left;
newNode.right = this.right.left;
this.value = this.right.value;
this.right = this.right.right;
this.left = newNode;
}右旋转
当 左子树深度 – 右子树深度 > 1 时,进行左旋转,将其换为 AVL 树。
右旋转与左旋转类似,只是操作相反。
- 创建一个新的节点(newNode),值与当前根节点(rootNode)相同
newNode.value = rootNode.value - 把新节点的右指针设为 rootNode 的右指针指向的节点
newNode.right = rootNode.right - 把新节点的左指针设为 rootNode 的左指针的右指针指向的节点
newNode.left = rootNode.left.right - 把 rootNode 的值设为它的左指针指向节点的值
rootNode.value = rootNode.left.value - 把 rootNode 的左指针设为它的左指针的左指针指向的节点
rootNode.left = rootNode.left.left - 把 rootNode 的右指针设为新节点 newNode
rootNode.right = newNode
public void rightRotate() {
Node newNode = new Node(this.value);
newNode.right = this.right;
newNode.left = this.left.right;
this.value = this.left.value;
this.left = this.left.left;
this.right = newNode;
}双旋转
当根节点左子树的左子树的高度小于根节点左子树的右子树的高度(depth(root.left.left)<depth(root.left.right))时,进行旋转后并没有达到平衡,因此,进行双旋转。例如下面这棵树:depth(root.left.left) = 1< depth(root.left.right) = 2
/*
* 10
* / \
* 7 11
* / \
* 6 8
* \
* 9
* */对于满足左旋转(右子树深度 – 左子树深度 > 1)且满足双旋转条件(右节点的左子树的深度 > 右节点的右子树深度)时:
- 先对根节点的右节点进行右旋转
rightRotate(rootNode.right) - 再对根节点进行左旋转
leftRotate(rootNode)
对于满足右旋转(左子树深度 – 右子树深度 > 1)且满足双旋转条件(左节点的右子树的深度 >左节点的左子树深度)时:
- 先对根节点的左节点进行左旋转
leftRotate(rootNode.left) - 再对根节点进行右旋转
rightRotate(rootNode)
完整实现
import java.util.Objects;
public class AVLTree {
public static void main(String[] args) {
Tree avlTree = new Tree();
int[] arr = {10, 11, 7, 6, 8, 9};
//{4, 3, 6, 5, 7, 8} can test leftRotate
//{10, 12, 8, 9, 7, 6} can test rightRotate
//{10, 11, 7, 6, 8, 9} and {2, 1, 6, 5, 7, 3} can test doubleRotate
for (int j : arr) {
avlTree.add(new Node(j));
}
avlTree.inOrder();
System.out.println("root depth:" + avlTree.getRootDepth());
System.out.println("left depth:" + avlTree.getLeftDepth());
System.out.println("right depth:" + avlTree.getRightDepth());
}
}
class Tree {
Node root;
/**
* Add a node to BST
*
* @param node the node to add
*/
public void add(Node node) {
if (node == null) {
System.out.println("Node is null");
} else {
if (root == null) {
root = node;
} else {
root.add(node);
if (root.getRightDepth() - root.getLeftDepth() > 1) {
if (root.right.getLeftDepth() > root.right.getRightDepth()) {
root.right.rightRotate();
}
root.leftRotate();
}
if (root.getLeftDepth() - root.getRightDepth() > 1) {
if (root.left.getRightDepth() > root.left.getLeftDepth()) {
root.left.leftRotate();
}
root.rightRotate();
}
}
}
}
/**
* in Order the whole BST recursively
*/
public void inOrder() {
if (root == null) {
System.out.println("root is null!");
return;
}
root.inOrder();
System.out.println();
}
/**
* get the parent of a node
*
* @param searchValue a child node
* @return parent node
*/
public Node recursionSearchParent(int searchValue) {
if (searchValue == root.value) {
return null;
}
return root.recursionSearchParent(searchValue);
}
/**
* get the parent of a node
*
* @param searchValue a child node
* @return parent node
*/
public Node whileSearchParent(int searchValue) {
if (searchValue == root.value) {
return new Node();
}
return root.whileSearchParent(searchValue);
}
/**
* search the node
*
* @param searchValue the value want to search
* @return a node and the node's value equals the search value
*/
public Node recursionSearchNode(int searchValue) {
return root.recursionSearchNode(searchValue);
}
/**
* delete a node
*
* @param targetNode a node to delete, can generate by recursionSearchNode()
*/
public void deleteNode(Node targetNode) {
if (Objects.equals(targetNode, root)) { //if it is root node
Node successor = root.searchSuccessor(targetNode); //find the successor
Node successorParent = targetNode.whileSearchParent(successor.value); //find the parent of the successor
targetNode.value = successor.value; //change the root.value
if (successor.value > successorParent.value) { //judge successor is right or left sub node
// then remove the parent's pointer
successorParent.right = null;
} else {
successorParent.left = null;
}
} else { //if it is not a root node
root.deleteNode(targetNode);
}
}
public int getRootDepth() {
return root.getDepth();
}
public int getRightDepth() {
return root.getRightDepth();
}
public int getLeftDepth() {
return root.getLeftDepth();
}
}
class Node {
int value;
Node left;
Node right;
public Node getLeft() {
return left;
}
public Node getRight() {
return right;
}
//constructor
public Node() {
}
public Node(int value) {
this.value = value;
}
/**
* add a node to BST
*
* @param node a node to add
*/
public void add(Node node) {
if (node == null) {
System.out.println("Node is null");
} else {
if (this.value < node.value) {
if (this.right == null) {
this.right = node;
} else {
right.add(node);
}
} else {
if (this.left == null) {
this.left = node;
} else {
left.add(node);
}
}
}
}
/**
* inorder, sorted
*/
public void inOrder() {
if (this.left != null) {
this.left.inOrder();
}
System.out.print(this.value + ",");
if (this.right != null) {
this.right.inOrder();
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
/**
* search a node's parent
*
* @param value node's value
* @return parent node
*/
public Node recursionSearchParent(int value) {
//search from a node to the leaf node
//one of child node's value == value, return this node
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
//search right
if (this.value < value && this.right != null) {
return right.recursionSearchParent(value);
}
//search left
if (this.value >= value && this.left != null) {
return left.recursionSearchParent(value);
}
}
//not found
return new Node();
}
/**
* search a node's parent
*
* @param searchValue the node's value
* @return parent node
*/
public Node whileSearchParent(int searchValue) {
Node tempNode = this;
while (true) { //find until leaf node
if (tempNode.left != null && tempNode.left.value == searchValue || tempNode.right != null && tempNode.right.value == searchValue) {
return tempNode;
} else if (tempNode.value < searchValue && tempNode.right != null) {
tempNode = tempNode.right;
} else if (tempNode.value >= searchValue && tempNode.left != null) {
tempNode = tempNode.left;
} else if (tempNode.left == null && tempNode.right == null) {
return new Node();
}
}
}
/**
* search a node
*
* @param value node's value
* @return the node, which value == value
*/
public Node recursionSearchNode(int value) {
if (this.value == value) {
return this;
}
if (this.value < value && this.right != null) {
return this.right.recursionSearchNode(value);
}
if (this.value > -value && this.left != null) {
return this.left.recursionSearchNode(value);
}
return null;
}
/**
* delete a node in BST
* only use this method can not delete root node
*
* @param targetNode a node to delete, can generate by recursionSearchNode()
*/
public void deleteNode(Node targetNode) {
Node targetNodeParent = recursionSearchParent(targetNode.value);
//case 0 targetNode is a leaf node
if (targetNode.left == null && targetNode.right == null) {
if (targetNode.value > targetNodeParent.value) {
targetNodeParent.right = null;
} else {
targetNodeParent.left = null;
}
}//case 1 targetNode has one sub node
else if (targetNodeParent.right == null && targetNodeParent.left != null || targetNodeParent.right != null && targetNodeParent.left == null) {
if (targetNodeParent.value < targetNode.value) { //targetNode on the right of parent
targetNodeParent.right = searchSuccessor(targetNode);
} else { //targetNode on the left
targetNodeParent.left = searchSuccessor(targetNode);
}
}//case 2 targetNode has two sub nodes
else {
//get successor and successor's parent
Node successor = searchSuccessor(targetNode);
Node successorParent = recursionSearchParent(successor.value);
// delete the pointer to successor
if (Objects.equals(successorParent.right, successor)) {
successorParent.right = null;
} else {
successorParent.left = null;
}
// make the target node parent point to successor
if (Objects.equals(targetNodeParent.right, targetNode)) {
targetNodeParent.right = successor;
} else {
targetNodeParent.left = successor;
}
//make the pointer point to original node
successor.left = targetNode.left;
successor.right = targetNode.right;
}
}
/**
* look for successor, smallest in right subtree (inorder successor)
* the biggest in left subtree also can work (predecessor)
*
* @param targetNode a node want to find successor
* @return the node's successor
*/
public Node searchSuccessor(Node targetNode) {
Node successor;
//case 0
if (targetNode.left != null && targetNode.right == null) {
return targetNode.left;
}
if (targetNode.left == null && targetNode.right != null) {
return targetNode.right;
}
//case 1
if (targetNode.left != null) { // now (targetNode.right != null) is always true
successor = targetNode.right;
while (successor.left != null) {
successor = successor.left;
}
return successor;
}
//if (targetNode.left==null && targetNode.right==null)
return null;
}
/**
* use current node as root and get the depth of the tree
*
* @return depth of current node
*/
public int getDepth() {
return Math.max(left == null ? 0 : left.getDepth(), right == null ? 0 : right.getDepth()) + 1;
}
/**
* use current's left node as root and get the depth of the tree
*
* @return depth of current's left node
*/
public int getLeftDepth() {
if (left == null) {
return 0;
} else {
return left.getDepth();
}
}
/**
* use current's right node as root and get the depth of the tree
*
* @return depth of current's right node
*/
public int getRightDepth() {
if (right == null) {
return 0;
} else {
return right.getDepth();
}
}
/**
* use current node as root node and left rotate
*/
public void leftRotate() {
Node newNode = new Node(this.value);
newNode.left = this.left;
newNode.right = this.right.left;
this.value = this.right.value;
this.right = this.right.right;
this.left = newNode;
}
/**
* use current node as root node and right rotate
*/
public void rightRotate() {
Node newNode = new Node(this.value);
newNode.right = this.right;
newNode.left = this.left.right;
this.value = this.left.value;
this.left = this.left.left;
this.right = newNode;
}
/*
* 10
* / \
* 7 11
* / \
* 6 8
* \
* 9
* */
/*
public void doubleRotate() {
this.left.leftRotate();
this.rightRotate();
}
*/
}多叉树 Muliway Tree
二叉树操作效率较高,但也存在问题:二叉树需要把数据加载到内存,要进行多次IO操作,节点多时,二叉树的高度会很大,会降低操作速度。
多叉树允许每个节点有更多的数据项和更多的子节点
B 树
通过重新组织节点,降低树的高度,减少I/O读写次数来提升效率,B树的所有叶子节点都在同一层
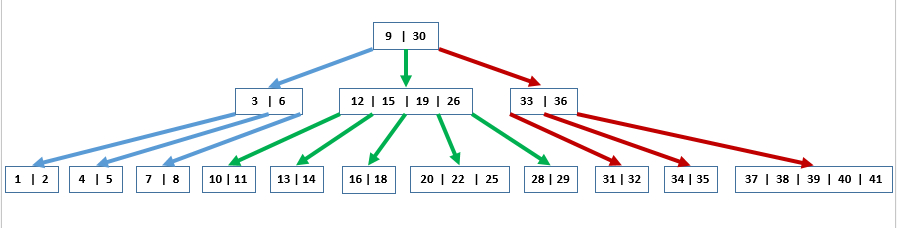
2-3树
- 有 3 个子节点的节点称为 “3 节点”,要么有3个子节点,要么没有子节点
- 有 2 个子节点的节点称为 “2 节点”,要么有2个子节点,要么没有子节点
- 2-3 树是最简单的一种 B 树,B树的所有叶子节点都在同一层
- 2-3 树是一种由 “2 节点” 和 “3 节点” 构成的树
2节点和普通二叉树相同,3节点中:
- 左子节点的值小于父节点两元素的最小值
- 中间子节点的值介于父节点的两个值之间
- 右子节点的值大于父节点两元素的最大值
B+树
数据只能在叶子节点非叶子节点相当于是叶子节点的索引,常见与文件索引系统和数据库